
Exact P-Values for Z-Testsįor the first row (never married), SPSS claims that the Bonferroni corrected p-value for comparing column percentages A and D is p = 0.020. CTABLES /VLABELS VARIABLES=marit educ DISPLAY=DEFAULT /TABLE marit BY educ /CATEGORIES VARIABLES=marit ORDER=A KEY=VALUE EMPTY=INCLUDE TOTAL=YES POSITION=AFTER /CATEGORIES VARIABLES=educ ORDER=A KEY=VALUE EMPTY=INCLUDE /CRITERIA CILEVEL=95 /COMPARETEST TYPE=PROP ALPHA=0.05 ADJUST=BONFERRONI ORIGIN=COLUMN INCLUDEMRSETS=YES CATEGORIES=ALLVISIBLE MERGE=NO STYLE=SIMPLE SHOWSIG=YES. *Contingency table with Bonferroni corrected z-tests (exact p-values) in separate table. Selecting it results in the syntax below. For our example table with 5 columns, each p-value is multiplied by \(0.5\cdot5(5 - 1) = 10\) before evaluating if it's smaller than the chosen alpha level of 0.05.Ĭustom Tables has an option to create a table containing the exact p-values for all pairwise z-tests. The percentage of people who never married is significantly higher for those who only completed middle school (46.2% from n = 39) than for those who completed a Master’s degree (16.7% from n = 54).Īgain, all z-tests use α = 0.05 after Bonferroni correcting their p-values for the number of columns in the table. The D in column A indicates that these 2 percentages Somewhat confusingly, SPSS flags the frequencies instead of the percentages. If 2 proportions differ significantly, then the higher is flagged with the column letter of the lower. Within each row, each possible pair of column proportions is compared using a z-test. Now, for normal 2-way contingency tables, the “innermost subtable” is simply the entire table. Tests are adjusted for all pairwise comparisons within a row of each innermost subtable using the Bonferroni correction.” Significance level for upper case letters (A, B, C). For each significant pair, the key of the category with the smaller column proportion appears in the category with the larger column proportion. Let's first try and understand what the footnote says: “Results are based on two-sided tests. Custom Tables with Pairwise Z-Tests Output CTABLES /VLABELS VARIABLES=marit educ DISPLAY=DEFAULT /TABLE marit BY educ /CATEGORIES VARIABLES=marit ORDER=A KEY=VALUE EMPTY=INCLUDE TOTAL=YES POSITION=AFTER /CATEGORIES VARIABLES=educ ORDER=A KEY=VALUE EMPTY=INCLUDE /CRITERIA CILEVEL=95 /COMPARETEST TYPE=PROP ALPHA=0.05 ADJUST=BONFERRONI ORIGIN=COLUMN INCLUDEMRSETS=YES CATEGORIES=ALLVISIBLE MERGE=YES STYLE=SIMPLE SHOWSIG=NO. *Contingency table with pairwise z-tests via CTABLES. Next, our z-tests are found in the Test Statistics tab shown below.Ĭompleting these steps results in the syntax below. We recommend you add totals for education levels as well. You probably want to select both frequencies and column percentages for education level. The figure below suggests some basic steps. They're found underīut only if you have a Custom Tables license. Option 2 - Custom TablesĪ second option for obtaining “post hoc tests” for chi-square tests are Custom Tables. This holds for all tests reported in this table. Or -reversely- only z-tests yielding an uncorrected p < 0.0 05 are labeled “significant”. Which means that each p-value is multiplied by 10 and only then compared to alpha = 0.05. Now, a Bonferroni correction is applied for the number of tests within each row.

It doesn't differ significantly from any cells labeled “a”, “b” or both. The frequency of people with a Bachelor’s degree who never married (n = 21 or 25.0%) is labeled both “a” and “b”. This means that 46.2% differs significantly from 16.7%. For those with a Master’s degree, 16.7% never married and its frequency of 9 is not labeled “a”.
Within each row, percentages that don't share a subscriptįor example, the percentage of people with middle school who never married is 46.2% and its frequency of n = 18 is labeled “a”. If they don't differ, they get a similar subscript. These also apply to the percentages shown in the table: within each row, each possible pair of percentages is compared using a z-test. These conclusions are based on z-tests for independent proportions.
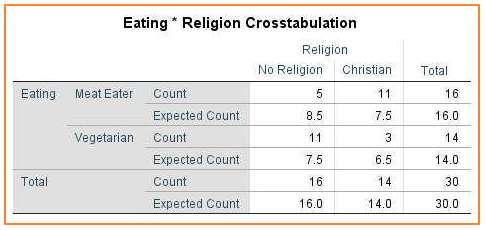
CROSSTABS with Pairwise Z-Tests Outputįirst off, take a close look at the table footnote: “Each subscript letter denotes a subset of Education Level categories whose column proportions do not differ significantly from each other at the.

Running this simple syntax results in the table shown below. *bprop = Bonferroni adjusted z-tests for column proportions. crosstabs marit by educ /cells count column bprop.


 0 kommentar(er)
0 kommentar(er)
